Profesor en Línea

Tu ayuda para las tareas

Como se supone que ya sabemos, se llama efecto Doppler a las variaciones aparentes en la frecuencia de una onda cualquiera (sonora, luminosa, en el agua, etcétera), causadas por el movimiento ya sea de la fuente emisora, ya sea del receptor de la onda sonora o de ambos.

A modo de recordatorio, analicemos la siguiente escena:

La moto (es la fuente sonora) emite un sonido, supongamos de 200 Hz de frecuencia, que viaja por el espacio hacia todas direcciones a una velocidad de 343 metros por segundo. A su vez, la moto lleva una velocidad propia, que supondremos de 80 km por hora (unos 22 m/s).

¿Qué sucede con los receptores respecto a la frecuencia con que perciben el sonido de la moto?

Veamos:

Todo depende de las velocidades de los involucrados.

La chica de la izquierda está en reposo, respecto a ella, el sonido debería llegar a la velocidad de 343 m/s, pero resulta que el emisor del sonido (la moto) se aleja de ella a 22 m/s; por lo tanto, a ella le llega el sonido solo a 321 m/s (343 menos 22), por lo tanto percibirá un sonido de menor frecuencia (ondas más largas, tono menos agudo).

El muchacho de la derecha camina, supongamos a 3 m/s, hacia la moto. Respecto a este muchacho, el sonido viaja hacia él a 343 m/s, más los 22 m/s de la moto y más los 3 m/s de su caminar hacia la moto; por lo tanto, percibirá un sonido de mayor frecuencia, ondas más cortas, tono más agudo).

Entendida esta relación entre las velocidades, ahora mostraremos cómo es posible obtener ecuaciones que nos permiten calcular las variaciones de frecuencia percibidas por un receptor.

Para no complicar vuestra existencia estudiantil estableceremos que la siguiente fórmula general permite hallar la frecuencia que percibirá el receptor u observador:

Donde :

fo = frecuencia que percibe el observador (también se usa como fr o frecuencia de la señal recibida)

ff = frecuencia real que emite la fuente (también se usa como fe o frecuencia de la señal emitida)

vs = velocidad del sonido (343 m/s)

vo = velocidad del observador (también se usa como vr o velocidad del receptor)

vf = velocidad de la fuente (también se usa como ve o velocidad del emisor)

Debemos fijar la atención en los signos + (más) y – (menos) de la ecuación.  Notemos que en el numerador aparece como ± (más menos) y en el denominador aparece invertido (menos más). Esta ubicación de signos es muy importante ya que usar uno u otro depende de si el observador se acerca o se aleja de la fuente emisora de sonido.

Importante:

 Si el observador se acerca a la fuente emisora, el signo en el numerador será + (más) y simultáneamente el signo en el denominador será – (menos).

Ahora, si el observador se aleja de la fuente emisora, el signo en el numerador será – (menos) y simultáneamente el signo del denominador será + (más).

Veamos  un ejemplo:

La radio emite un sonido con frecuencia de 440 Hz

El mono (perdón, el receptor u observador) camina hacia la fuente (la radio, fija) con velocidad  de 20 m/s

Pregunta: ¿con qué frecuencia recibe el sonido el receptor?

Analicemos los datos que tenemos:

 fo =  x (desconocida): frecuencia que percibe el observador

ff =  440 Hz:  frecuencia real que emite la fuente

vs = 343 m/s: velocidad del sonido

vo = 20 m/s: velocidad del observador (con signo + ya que se acerca a la fuente)

vf = 0:  velocidad de la fuente (fuente en reposo)

Usemos nuestra fórmula y coloquemos los valores:

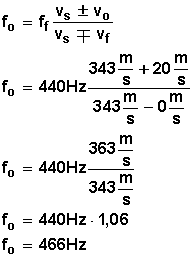
Nótese que la velocidad de la fuente (la radio) es 0 (cero) pues se haya en un lugar fijo, no tiene movimiento.

Respuesta:

El receptor (el mono) percibe el sonido con una frecuencia de 466 Hz.

La clave para resolver este y otros ejercicios está en saber colocar el signo de suma o de resta a la velocidad del receptor y la del emisor.

Otro ejemplo:

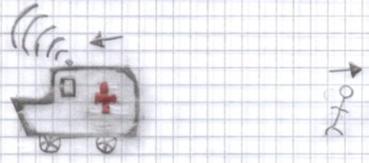
La sirena de la ambulancia emite un sonido cuya frecuencia es 200 Hz.

La ambulancia viaja a 80 m/s (alejándose del receptor)

El receptor (el mono) se aleja de la ambulancia a velocidad de 5 m/s (con signo – pues se aleja de la fuente)

Pregunta: ¿con qué frecuencia recibe el sonido el receptor?

Hacemos lo mismo del ejemplo anterior, usamos la fórmula y ponemos los valores:

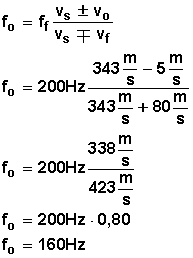
Respuesta:

El receptor (el mono) percibe el sonido con una frecuencia de 160 Hz.

Cálculo de las longitudes de onda

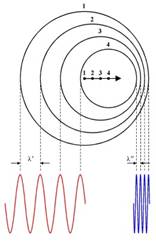
También se debe considerar que, por el efecto Doppler, por delante del emisor los frentes de onda se estrechan (disminuye la longitud de la onda), generando un aumento de frecuencia. Por detrás del emisor se produce el efecto contrario, los frentes de onda se separan (aumenta la longitud de la onda) y por tanto la frecuencia disminuye.

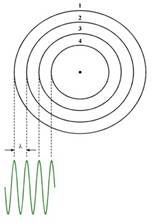
Para poder expresar con números el fenómeno descrito anteriormente, consideremos los esquemas siguientes:

Fuente emisora y observador están fijos: la frecuencia emitida es la misma percibida.		Fuente en movimiento: hacia atrás se percibe menor frecuencia; hacia adelante, se percibe mayor frecuencia.

En el primer caso, las perturbaciones generadas por la fuente tienen la misma frecuencia en el lugar en que se originan que en el lugar donde son percibidas. (La fuente está en reposo con respecto al observador.) En este caso la longitud de la onda es .

En el segundo caso, la fuente se mueve: el observador del cual la fuente se aleja percibe las perturbaciones como si la onda tuviera la longitud (mayor longitud); el observador al cual la fuente se dirige lo hace como si su longitud fuera (menor longitud).

El cálculo de estas longitudes de onda a partir de la velocidad de propagación de la onda, la velocidad de la fuente (f) y el período (tiempo T) se hace con las siguientes fórmulas:

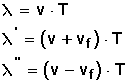
Volver a: Sonido: Efecto Doppler

Fuentes Internet:

http://wdict.net/es/word/efecto+doppler/

http://www.angelfire.com/ia3/doppler/

Ver animación para mejor comprensión del efecto Doppler, en

http://www.santillana.cl/fis1/fisica1u1t3.htm

Es propiedad: www.profesorenlinea.cl - Registro N° 188.540